이진 트리는 각 노드가 왼쪽, 오른쪽 최대 두개의 자식 노드만을 가질 수 있는 트리이다.
따라서 이진 트리는 자식 노드들의 배열 대신 두개의 포인터 left, right를 담는 객체로 구현된다.
이진 검색 트리는 각 노드의 왼쪽 서브트리에는 해당 노드의 원소보다 작은 원소를 가진 노드들이 있고,
오른쪽 서브트리에는 해당 노드의 원소보다 큰 원소를 가진 노드들이 있는 트리이다.
n개의 노드가 있을 때, 원하는 원소를 찾기 위해서 매번 후보의 수를 절반씩 줄여갈 수 있으므로
O(logN) 시간에 해결할 수 있을 것이다.
이진 검색 트리는 집합에 원소를 삽입하거나 삭제할 때 진가를 드러낸다.
원하는 원소를 찾거나, 최대, 최소 원소를 구하는 등의 구현은 정렬된 배열일 때도 쉽게 할 수 있다.
그러나 정렬된 배열에 하나의 원소를 삽입하거나 삭제하는 일은 다소 복잡하다.
BST에서는 그 작업들을 간단하게 할 수 있다.
BST는 원소의 삽입 순서에 따라 그 형태가 달라지게 된다.
정렬된 상태의 배열이 순서대로 입력되는 경우 BST는 한쪽으로 길게 치우친 형태를 하고 있을 것이다.
이 때는 O(logN)의 시간 내에 탐색을 하기가 불가능하다.
따라서 Tree와 Heap을 합친 형태인 Treap 자료구조를 통하여 균형잡힌 BST를 구현할 수 있다.
트립은 기본 BST가 원소에 해당하는 키값만 가지고있는 것과 다르게 우선순위를 가지고 있다.
우선순위는 키값의 대소관계나 입력 순서와 아무 관계없이 랜덤하게 정해진다.
트립은 항상 부모의 우선순위가 자식의 우선순위보다 높은 BST를 만든다.
즉, 모든 노드의 우선순위는 각자의 자식노드보다 크거나 같다는 의미이다.
트립의 구현
struct Node {
int key; // 노드의 키값
int priority; // 노드의 우선순위
int size; // 해당 노드를 루트로 하는 트리의 크기
Node *left, *right; // 노드의 왼쪽, 오른쪽 자식 노드 포인터
// Node 구조체 생성자
// 노드의 우선순위는 랜덤하게 지정해준다.
Node(const int _key) : key(_key), priority(rand()), size(1), left(NULL), right(NULL) {}
// 새로운 서브트리를 왼쪽 자식 서브트리로 변경
void setLeft(Node* newLeft) {
left = newLeft;
calcSize();
}
// 새로운 서브트리를 오른쪽 자식 서브트리로 변경
void setRight(Node* newRight) {
right = newRight;
calcSize();
}
// 트리의 사이즈 계산
void calcSize() {
size = 1;
if (left) size += left->size;
if (right) size += right->size;
}
};기존 BST와 다른 점은 key값 외에 우선순위를 가지고 있다는 점이다.
또한, 자신을 루트로 하는 트리에 포함된 노드의 수를 나타내는 size 변수가 존재한다.
이 값을 이용하면 k번째 원소를 찾는 연산이나 X보다 작은 원소를 세는 연산 등을 쉽게 구현할 수 있다.
노드의 추가와 '쪼개기' 연산
root를 루트로 하는 트리에 새로운 노드 node를 추가하고 싶다고 하자.
우선, root의 우선순위와 node의 우선순위를 비교해야 한다.
만약 root의 우선순위가 node의 우선순위보다 높다면, node는 root 아래로 들어가야 한다.
이 때 왼쪽 서브트리로 들어갈지, 오른쪽 서브트리로 들어갈지는
node의 key값과 root의 key값을 비교하여 정해주면 된다.
그 이후엔 해당 서브트리에 node를 추가하는 과정을 재귀적으로 진행해주면 된다.
node의 우선순위가 root의 우선순위보다 높은 경우엔 node가 루트가 되어야 한다.
그러면 root를 루트로 하는 트리를 왼쪽 서브트리와 오른쪽 서브트리로 쪼개주어야 한다.
이 때 트리를 쪼개는 기준은 node의 키값이 된다.
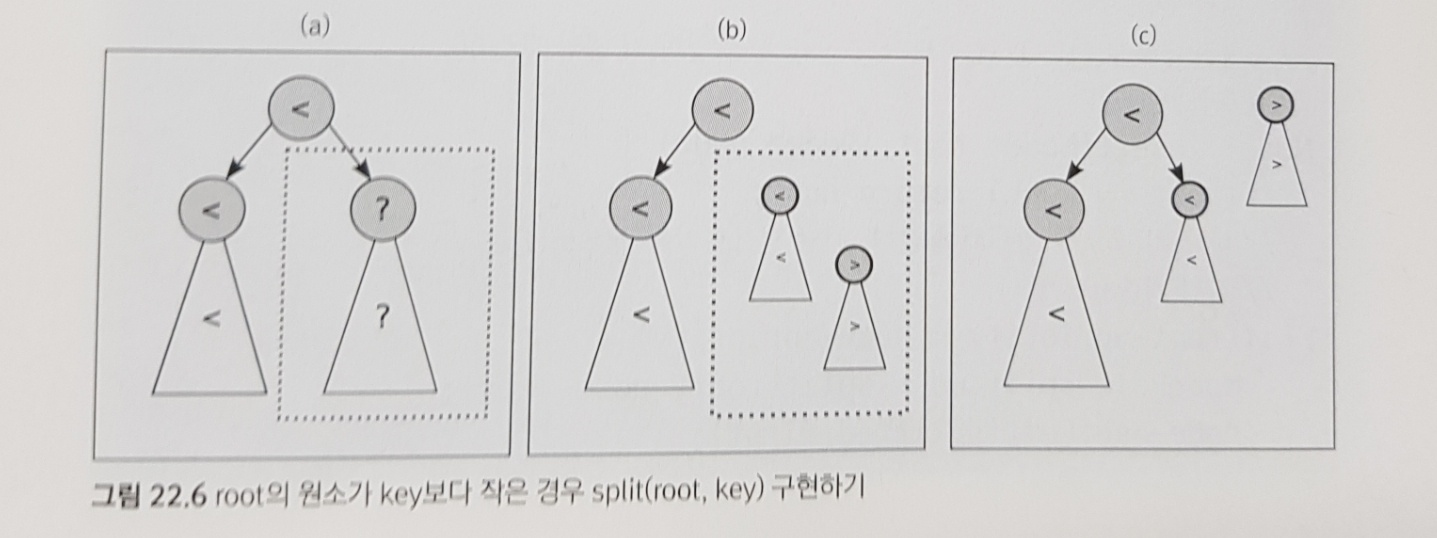
만약 root의 키값이 node의 키값보다 작으면
root의 왼쪽 서브트리는 당연히 node의 키값보다 작으므로 오른쪽 서브트리만 쪼개주면 된다.
그러면 다시 오른쪽 서브트리를 node의 키값을 기준으로 쪼개주어
쪼갠 트리의 왼쪽 트리는 기존 root의 오른쪽 서브트리로 다시 넣어주고, 오른쪽 트리는 node의 오른쪽 서브트리가 된다.
이 과정을 재귀호출로 반복하면 된다.
typedef pair<Node*, Node*> NodePair; // 쪼갠 트리의 왼쪽 트리, 오른쪽 트리 쌍
// key 값을 기준으로 node를 루트로 하는 트리를 쪼갬
NodePair splitNode(Node* node, int key) {
// base case : 노드가 존재하지 않으면 빈 페어 리턴
if (node == NULL) return NodePair(NULL, NULL);
// node의 키값이 key보다 작으면 node의 오른쪽 서브트리를 쪼개야함
if (node->key < key) {
NodePair rs = splitNode(node->right, key);
// 오른쪽 서브트리를 쪼개서 나온 key값보다 작은 서브트리는 다시 node의 오른쪽 서브트리가 됨
node->setRight(rs.first);
return NodePair(node, rs.second);
}
// node의 키값이 key보다 작지 않으면 node의 왼쪽 서브트리를 쪼개야함
NodePair ls = splitNode(node->left, key);
node->setLeft(ls.second);
return NodePair(ls.first, node);
}
// root를 루트로 하는 트리에 node를 추가하여 새로운 트리의 루트를 리턴함
Node* insertNode(Node* root, Node* node) {
// base case : root가 빈 노드이면 node가 루트가 됨
if (root == NULL) return node;
// root의 우선순위가 node의 우선순위보다 작으면 root를 루트로 하는 트리를 쪼개야 한다.
if (root->priority < node->priority) {
NodePair splitted = splitNode(root, node->key);
node->setLeft(splitted.first);
node->setRight(splitted.second);
return node;
}
// 그렇지 않으면 root와 node의 키값을 비교한다.
// node의 키값이 더 작으면 node를 왼쪽 서브트리에 추가한다.
else if (root->key > node->key) {
root->setLeft(insertNode(root->left, node));
}
else {
root->setRight(insertNode(root->right, node));
}
return root;
}
노드의 삭제와 '합치기' 연산
root를 루트로 하는 트리에서 key를 키값으로 가지고 있는 노드를 삭제한다고 하자.
우선 root의 키값과 key를 비교해서 root의 키값이 더 크면 왼쪽 서브트리에서 찾아서 삭제해야 한다.
반대의 경우는 오른쪽 서브트리에서 찾아서 삭제해야 한다.
이는 재귀호출을 통해 쉽게 구현할 수 있다.
삭제할 노드가 자식 노드를 가지고 있을 때
자식 서브트리들을 합쳐 새로운 트리를 만든 뒤,
이 트리를 삭제할 노드를 루트로 하는 트리와 바꿔치기 하면 된다.
이 때 트립의 경우 두 자식 서브트리의 루트의 우선순위를 비교하여 어느쪽이 루트가 될지 정해주어야 한다.
// a노드를 루트로 하는 트리와 b노드를 루트로 하는 트리를 합쳐줌
Node* merge(Node* a, Node* b) {
if (a == NULL) return b;
if (b == NULL) return a;
// 두 서브트리의 루트의 우선순위를 비교한다.
// a의 우선순위가 더 높다면 a가 루트가 되고,
// 다시 a의 오른쪽 서브트리와 b를 합친 결과를 오른쪽 서브트리로 한다.
if (a->priority > b->priority) {
a->setRight(merge(a->right, b));
return a;
}
// 반대의 경우 b가 루트가 되고, 다시 b의 왼쪽 서브트리와 a를 합친 결과를 왼쪽 서브트리로 한다.
b->setLeft(merge(a, b->left));
return b;
}
// root를 루트로 하는 트리에 key를 키값으로 하는 노드를 삭제하고 루트를 리턴함
Node* erase(Node* root, int key) {
if (root == NULL) return root;
// root의 키값이 key와 일치하면 root를 지운다.
if (root->key == key) {
Node* ret = merge(root->left, root->right);
delete root;
return ret;
}
// root의 키값이 key보다 작으면 오른쪽 서브트리에서 찾아서 지운다.
if (root->key < key) {
root->setRight(erase(root->right, key));
}
else {
root->setLeft(erase(root->left, key));
}
return root;
}'DEVELOP > 알고리즘' 카테고리의 다른 글
| 8. 트리의 구현과 순회 - 트리에서 가장 긴 경로 찾기 (0) | 2019.07.16 |
|---|---|
| 8. 트리의 구현과 순회 - 트리 순회 순서 변경(traversal) 문제 (0) | 2019.07.16 |
| 8. 트리의 구현과 순회 (0) | 2019.07.16 |
| 7. 최단 경로 알고리즘 - 선거 공약(promises) 문제 (0) | 2019.03.12 |
| 7. 최단 경로 알고리즘 - 음주 운전 단속(drunken) 문제 (0) | 2019.03.12 |


